【FDTD】Maxwell方程式の空間領域での離散化

前回導いた下の式を、空間領域で離散化する。

$$ E_z^n = \frac{1 – \frac{\sigma\Delta t}{2\varepsilon}}{1 + \frac{\sigma\Delta t}{2\varepsilon}} E_z^{n-1} + \frac{\frac{\Delta t}{\varepsilon}}{1 + \frac{\sigma\Delta t}{2\varepsilon}} ( \displaystyle \frac{\partial H_y^{n – \frac{1}{2}}}{\partial x} – \displaystyle \frac{\partial H_x^{n – \frac{1}{2}}}{\partial y})$$

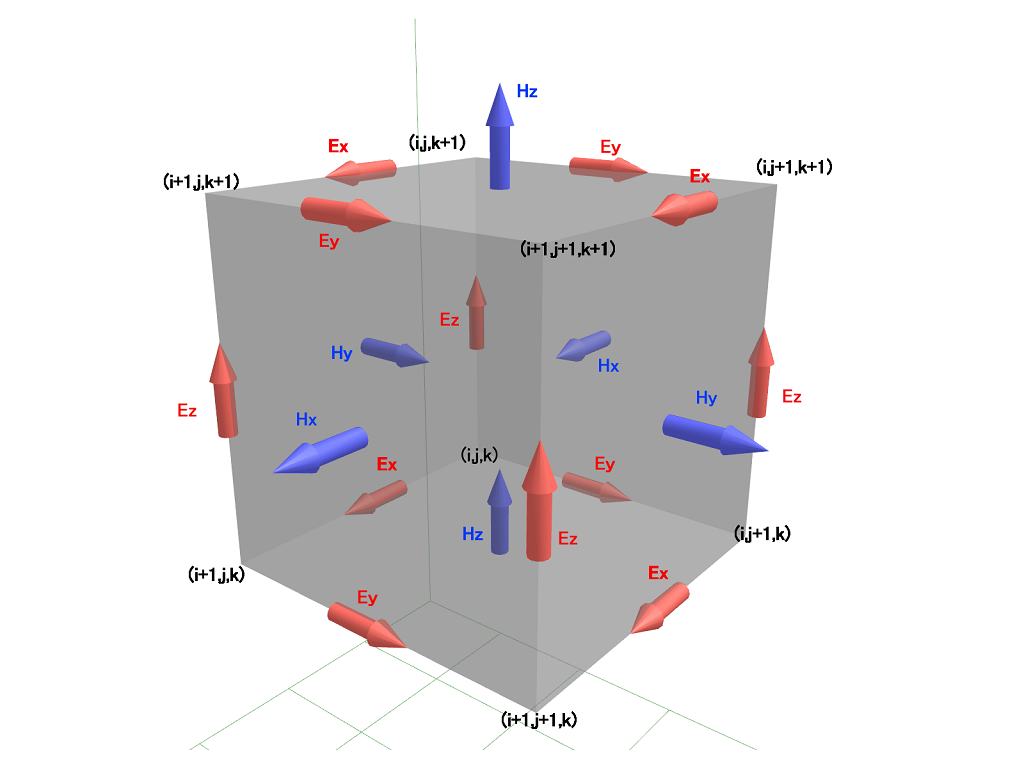
3次元の単位セルを再掲すると..

座標として、+1/2とか書くのは煩雑なので、以下のような置き換えをする。　コーディングするときは、座標は整数にする必要があるので、それも兼ねる。

Ex(i+1/2,j,k) → EX(I,J,K)、Ey(i,J+1/2,k) → EY(I,J,K)、Ez(i,j,k+1/2) → EZ(I,J,K)。
Hx(i,j+1/2,k+1/2) → HX(I,J,K)、Hy(i+1/2,j,k+1/2) → HY(I,J,K)、Hz(i+1/2,J+1/2,k) → HZ(I,J,K)
そして、例えばEx(i – 1/2,j,k)は、EX(I-1,j,k]とする。

以上のことを踏まえて、上の式を変形すると、

$$ E_z^n(I,J,K) = C_{ez}(I,J,K) E_z^{n-1}(I,J,K) + C_{ezx}(I,J,K) \lbrace H_y^{n-1/2}(I,J,K) – H_y^{n-1/2}(I-1,J,K) \rbrace \\ – C_{ezy}(I,J,K) \lbrace H_x^{n-1/2}(I,J,K) – H_x^{n-1/2}(I,J-1,K) \rbrace $$

対象解析空間の媒質が一様だとするとCez, Cezx, Cezyは定数となり、

$$ C_{ez}(I,J,K) = (1 – \frac{\sigma(I,J,K)\Delta t}{2\varepsilon(I,J,K)}) / (1 + \frac{\sigma(I,J,K)\Delta t}{2\varepsilon(I,J,K)}) $$

$$ C_{ezx}(I,J,K) = \frac{\Delta t}{\varepsilon(I,J,K)} / \lbrace (1 + \frac{\sigma(I,J,K)\Delta t}{2\varepsilon(I,J,K)})\Delta x\rbrace $$

$$ C_{ezy}(I,J,K) = \frac{\Delta t}{\varepsilon(I,J,K)} / \lbrace (1 + \frac{\sigma(I,J,K)\Delta t}{2\varepsilon(I,J,K)})\Delta y\rbrace $$

電界の他の成分や磁界も、同様に離散化できる。