4:1 Un-Unの解析（４）

相当前にやっていた４：１Un-Unの解析（これとかこれとかこれ）をまたやってみようと思う。　以前と重複した内容になるけど、ちょっとおさらい。

最初に理想的な状態でどうなるかを、Qucsでシミュレーションしてみる。

結合係数が１の場合で、コイルのインダクタンスが小さい場合、ここでは1uHとした。

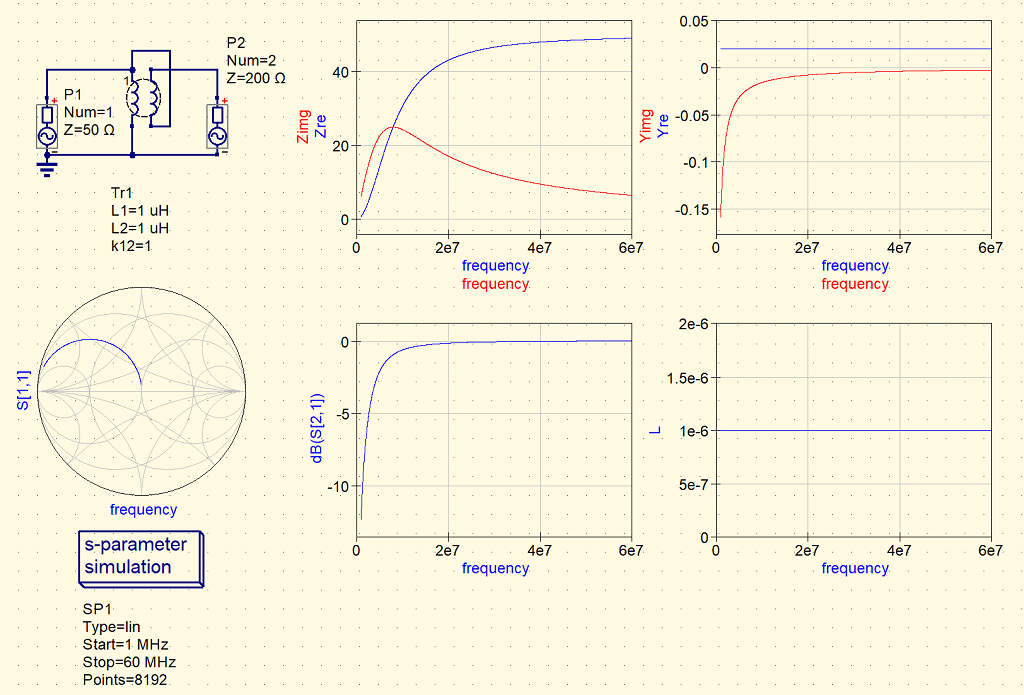
スミスチャートの軌跡を見ると、信号源からみたインピーダンスは、1uHのインダクタンスと200Ωの1/4の50Ωの並列接続であることがわかる。　S21を見ると、20MHz以下の周波数では挿入損失が大きくなっていることがわかる。

次に、インダクタンスを10uHに変えてみる。

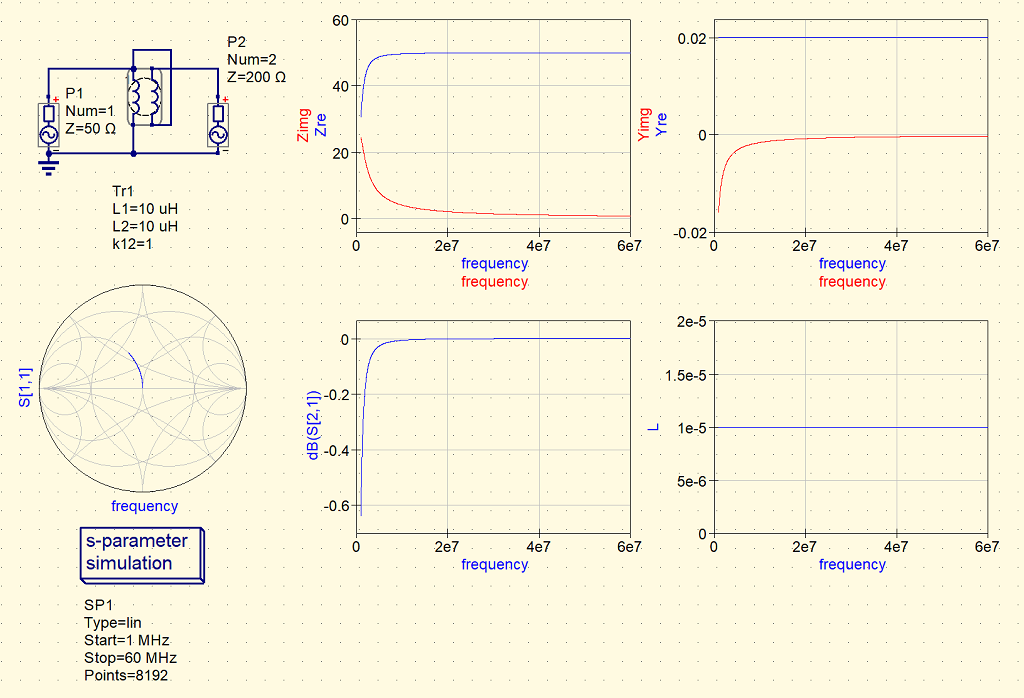
さっきと同じように、信号源から見たインピーダンスは、10uHと50Ωが並列接続になっている。　S21を見ると、低い周波数ではロスが増加しているものの、1uHの時とは違って挿入損失は、かなり改善されている。

理想的なインダクタは抵抗０Ωのはずなので、損失が発生するのはイマイチ理解に苦しむけど、まあ、とりあえずこういう結果が出た。　これだけで考えると、インダクタンスを大きくしてやらないと、低周波でのロスが大きくなるということなので、できるだけ巻き数を多くしてやればいいということになるけど、世の中そううまくはいかない。　

次に、結合係数を0.8にしてみる。

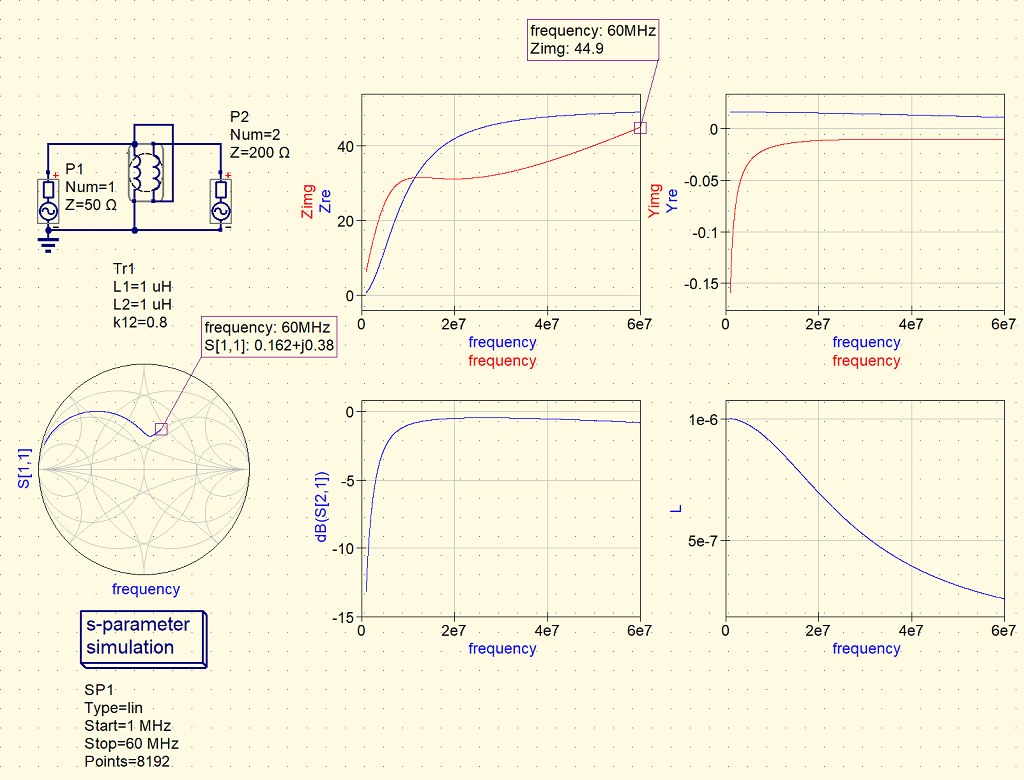
周波数の低い領域では、抵抗とインダクタの並列接続だが、周波数が高くなると抵抗とインダクタの直列接続に見える。

60MHzでのリアクタンスの値からインダクタンスを算出してみると、L=44.9/(2*Pi*60e6)=0.12uHとなり、これはL1*(1-k12)/2の値となっているように見える。

また、挿入損失は、高い周波数でも発生している。　これは、直列に入ったリーケージインダクタンスのためだと思われる。

次に、インダクタンスを10uHにしてみる。

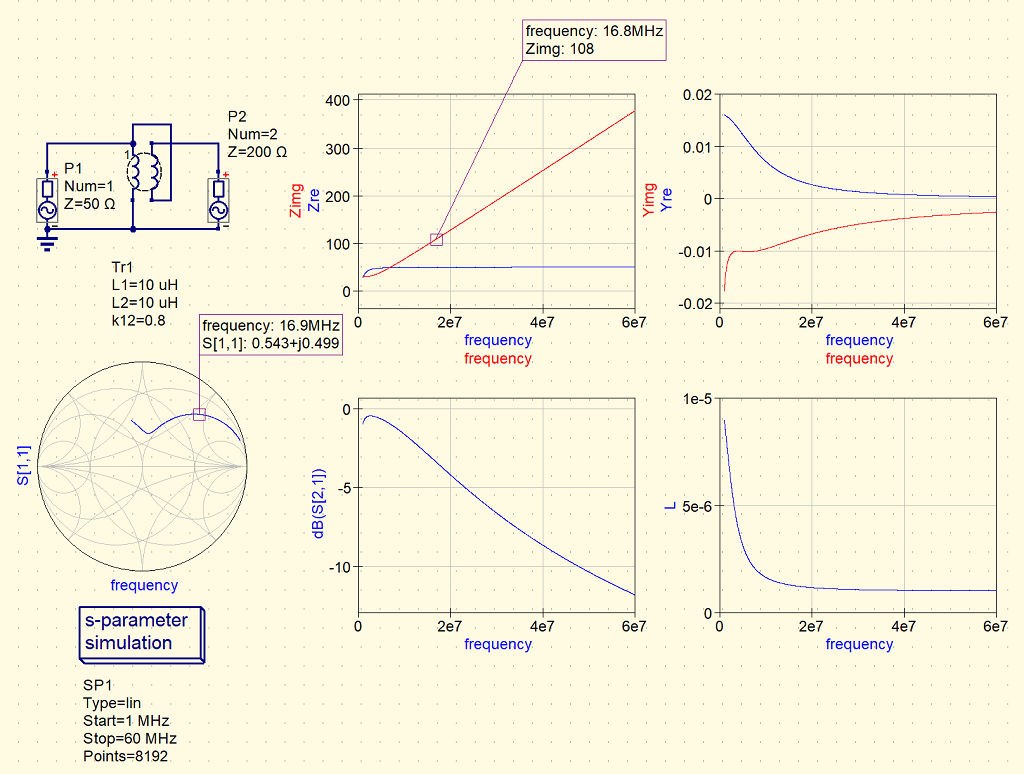
リーケージインダクタンスの影響が大きくなって、高い周波数での損失が大きくなってほぼ使用不可能になった。

現実には結合係数１はありえないので、インダクタンスの上限は制限されることになる。　

という訳で、インダクタンスの適正値が存在することが判った。　

以上の結果から考察すると、実際に作製した場合にどの程度の結合係数が実現できるかで、どの程度の広帯域なUn-Unが実現できるかが決まるということなのかな．．。

次は、実際にUn-Unを作成してみる。